Anomaly Transformer
논문: Anomaly Transformer: Time Series Anomaly Detection with Association Discrepancy
개요
시계열 이상 탐지 모델에 대해 찾아보았다.
인용수도 준수하고 Transformer를 활용한 논문이 눈에 들어와서 읽어보기로 했다.
찾아 본 영단어
Discrepancy: 차이
Adversarial: 적대적인
Conducive: 유리한
Taxonomy: 분류학
요약
Abstract
Transformer가 전체 구간에 대한 각 시점의 해석을 가능케하나, 이상점이 드물기 때문에 연관성을 구축하기 어려워 인접한 구간에 집중한다.
비지도 방식의 시계열 이상 탐지는 모델이 구별 기준을 도출해야해서 어려운 점이 있다. pointwise representation 또는 pairwise association으로 접근했던 이전 방식들과 달리, Transformer는 pointwise representation과 pairwise association를 통합하고 전체 구간에 대한 각 시점의 해석을 가능하게 한다. 하지만 이상점이 드물기 때문에 전체 구간에 대한 뾰족한 연관성을 구축하는 것은 어렵고, 따라서 인접한 구간에 집중할 것이다.
Anomaly Transformer은 Association Discrepancy를 활용하여 인접한 구간에 집중된 bias를 설정하고, 이상점에 대한 구별 가능성을 증폭시키기 위해 minimax strategy를 적용하였다.
인접한 구간에 집중된 bias는 Association Discrepancy로 도출하여 이상점에 대한 기준을 설정했다. 그리고 Association Discrepancy을 계산하기 위해 Anomaly Transformer을 제한한다. 이상점에 대한 구별 가능성을 증폭시키기 위해 minimax strategy를 Association Discrepancy에 적용했다. Anomaly Transformer는 비지도 시계열 이상 탐지 벤치마크에서 SOTA를 달성했다.
1 Introduction
시계열 이상 탐지는 복잡한 시간적 역학관계에서 의미있는 특징을 추출하고 희귀한 이상점을 구별할 수 있는 기준을 도출하는 것이 관건
시계열에서의 이상 탐지는 산업에서 중요하지만 이상점이 드물기 때문에 난이도와 비용적인 측면에서 데이터 라벨링하기 어렵다. 따라서 비지도 방식으로 눈을 돌렸지만, 복잡한 시간적 역학관계에서 의미있는 특징을 추출해야면서 희귀한 이상점을 구별할 수 있는 기준을 도출해야 하기 때문에 이 또한 어렵긴 하다.
다양한 시도가 있었지만 각각의 한계가 있었다.- 고전적 방법: 시간적 정보 고려 못함
- 신경망: 시간적 맥락의 포괄적인 설명 못함
- explicit association modeling: 미세한 연관성을 모델링 못함
- GNN: 복잡한 시간 패턴 학습 못함
- subsequence-based methods: 각 지점과 전체 구간 간의 미세한 시간적 연관성을 포착 못함
고전적으로 LOF, OC-SVM, SVDD 방법이 있는데, 시간적 정보를 고려하지 않아 실제 시나리오에 대한 일반화가 어렵다.
신경망을 활용하여 우수한 성능을 달성하였다.
잘 설계된 순환 네트워크를 통해 pointwise representations을 학습하고 reconstruction 또는 autoregressive task에 의해 self-supervised되는 것에 초점을 맞추고 있다.
여기서의 이상점 기준은 각 시점의 reconstruction 또는 prediction error이지만, 이상점이 드물기 때문에 pointwise representation는 복잡한 시간적 패턴에 대한 정보가 부족하고 정상점들에게 우세되어 구별력이 약해질 수 있다.
또한 reconstruction 또는 prediction error는 각 시점마다 계산되므로 시간적 맥락의 포괄적인 설명을 제공할 수 없다.
explicit association modeling을 기반의 이상 탐지 방법도 있다.
vector autoregression와 state space models 그리고 그래프를 활용하여 시계열을 각기 다른 시간 지점으로 정점으로 나타내고,random walk로 이상 탐지한 방법이 이에 포함된다.
일반적으로 이러한 고전적인 방법은 정보를 효과적으로 학습하고 미세한 연관성을 모델링하기 어렵다.
최근에는 GNN이 다중 변수 다변량 시계열에서 동적 그래프를 학습하는 데 적용되었는데, 표현력이 더 뛰어나지만 학습된 그래프는 여전히 단일 시간 지점으로 제한되어 복잡한 시간 패턴에는 여전히 부족하다.
또한, subsequence-based methods은 부분 시퀀스 간 유사도를 계산하여 이상점을 감지하기도 했다.
더 넓은 시간적 맥락을 탐색하더라도, 이러한 방법은 각 시간 지점과 전체 구간 간의 미세한 시간적 연관성을 포착하기 어렵다.
Transfomers를 비지도 시계열 이상 탐지에 적용- series-association: self-attention map을 통해 각 시간 점의 시간적 연관성 표현
- prior-association: Gaussian kernel을 통해 인접한 시점들이 연속성에 인해 연관되는 경향 계산
- Association Discrepancy: 각 시간 점의 prior-association과 series-association 간의 거리
- minimax 전략을 적용: Association Discrepancy의 정상-비정상 구별성을 증폭
본 논문에서 우리는 Transfomers를 비지도 시계열 이상 탐지에 적용할 것이다. Transfomers는 전체적 표현 및 long-range 관계를 통합 모델링하는 능력으로 자연어 처리, machine vision 및 시계열을 포함한 다양한 분야에서 큰 진전을 이루었다.
시계열에 Transfomers를 적용하면 각 시간 점의 시간적 연관성을 self-attention map에서 얻을 수 있으며, 이는 시간적 차원을 따라 모든 시간 점에 대한 연관성 가중치의 분포로 표현하게 된다.
각 시간 점의 연관성 분포는 시간적 맥락에 대한 보다 정보가 풍부한 설명을 제공할 수 있으며, 시계열의 주기 또는 추세와 같은 동적 패턴을 나타낼 수 있다.
위의 연관성 분포를 series-association이라고 하고, 이는 Transfomers에 의해 원본 시계열에서 발견될 수 있다.
더 나아가서, 이상점의 희귀성과 정상 패턴의 우세로 인해 이상점이 전체 구간과 강력한 연관성을 형성하는 것이 더 어렵다는 것을 관찰하였다.
이상점의 연관성은 연속성으로 인해 유사한 비정상적 패턴을 포함할 가능성이 더 높은 인접한 시간 점에 집중될 것이고, 이러한 인접 집중적 귀납적 편향은 prior-association이라고 한다.
반면에, 지배적인 정상 시간 점은 인접 영역에 제한되지 않고 전체 구간과 정보가 풍부한 연관성을 발견할 수 있다.
이 관찰을 기반으로, 연관성 분포의 본질적인 정상-비정상 구별성을 활용하려고 시도하였다.
이로 인해 각 시간 점에 대한 새로운 이상점 기준이 생기며, 이는 각 시간 점의 prior-association과 series-association 간의 거리로 측정되며, Association Discrepancy이라고 했다.
앞에서 언급한대로, 이상점의 연관성이 더 자주 인접 집중되기 때문에 이상점은 정상 시간 점보다 더 작은 Association Discrepancy을 나타낼 것이다.
이전 방법을 넘어서, 우리는 Transfomers를 비지도 시계열 이상점 탐지에 소개하고 연관 학습을 위해 Anomaly Transformer를 제안한다.
Association Discrepancy를 계산하기 위해, self-attention을 Anomaly-Attention으로 개선하였는데, 이는 각 시간 점의 prior-association과 series-association을 모델링하기 위한 두 개의 branch 구조를 포함한다.
prior-association은 각 시간 점의 인접 집중 귀납적 편향을 나타내기 위해 학습 가능한 Gaussian kernel을 사용하며, series-association은 원본 시리즈에서 학습된 self-attention 가중치에 해당한다.
또한, 두 개의 분기 사이에 minimax 전략을 적용하여 Association Discrepancy의 정상-비정상 구별성을 증폭시키고 새로운 연관 기반 기준을 더 구체화할 수 있다.
Anomaly Transformer는 세 가지 실제 응용 프로그램을 포함하는 여섯 가지 벤치마크에서 뛰어난 결과를 달성하였다.
2 Related Work
2.1 Unsupervised Time Series Anomaly Detection
비지도 시계열 이상 탐지 방법은 density estimation, clustering-based, reconstruction-based, autoregression-based와 같은 네 가지 범주로 나뉜다.
각 범주는 local density와 connectivity 계산, 클러스터 중심까지의 거리 측정, 재구성 reconstruction error 또는 미래 값을 예측하는 등의 다른 기법을 사용한다.
이 논문은 새로운 association-based criterion을 소개하며, temporal model co-design를 통해 정보를 효과적으로 학습하는 데 초점을 맞추었다.
2.2 Transformers For Time Series Analysis
Transformer는 자연어, 오디오, 시계열과 같은 sequential data 처리에 뛰어나며, 특히 시계열의 이상 감지에 유용하다.
GTA와 같은 방법은 Transformer와 그래프를 결합하여 센서 간의 관계를 학습한다.
Anomaly Transformer는 이러한 방법을 개선하여 self-attention 메커니즘의 변형인 Anomaly-Attention를 도입하여 데이터의 불일치를 더 잘 포착한다.
3 Method
비지도 시계열 이상 탐지란,
\(d\)개의 측정값으로 이루어진 시계열 \(X = \{x_1, x_2, ..., x_N\}, x_t \in \mathbb{R}^d\) 에서 \(x_t\)를 레이블 없이 이상치인지 판별하는 것
3.1 Anomaly Transformer
Overall Architecture
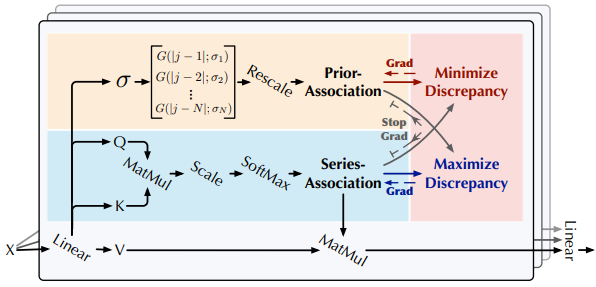
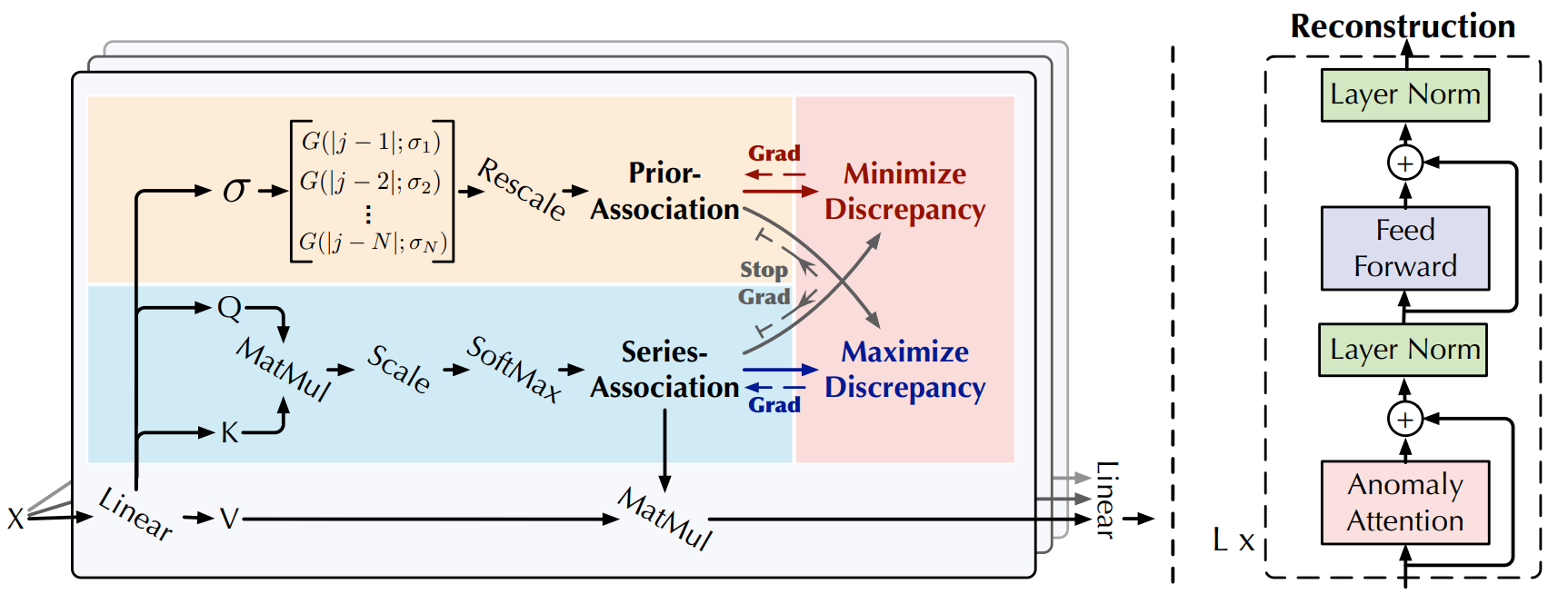Anomaly Transformer는 Anomaly-Attention 블록과 feed-forward 레이어를 번갈아 쌓는 특징을 가지고 있다.
이렇게 쌓은 구조는 깊은 다계층 특징에서의 근본적인 연관성을 학습하는 데 도움이 된다.
\(L\)개의 레이어로 이루어진 모델이 길이가 \(N\)인 시계열 \(X \in \mathbb{R}^{N×d}\)를 입력 받는다고 가정하자.
\(l\)번째 레이어의 전체 방정식은 다음과 같다.
여기서 \(X^l \in \mathbb{R}^{N×d_\text{model}}, l ∈ {1, ..., L}\) 는 \(d_\text{model}\) 채널을 가진 \(l\)번째 레이어의 출력을 나타낸다.
초기 입력 \(X^0 = \text{Embedding}(X)\)는 임베딩된 raw series를 나타낸다.
\(Z^l ∈ \mathbb{R}^{N×d_\text{model}}\) 는 \(l\)번째 레이어의 숨겨진 표현이다.
\(\text{Anomaly-Attention}(·)\)은 association discrepancy을 계산하는 데 사용된다.
Anomaly-Attention
single-branch self-attention 메커니즘은 prior-association과 series-association을 동시에 모델링할 수 없어서 두 개의 branch 구조를 갖는 Anomaly-Attention을 고안했다.
prior-association에 대해서는, 상대적 시간적 거리에 대한 prior를 계산하기 위해 학습 가능한 Gaussian kernel을 채택하였다.
Gaussian kernel의 unimodal 특성으로 인해, 이 설계는 인접한 수평에 더 많은 관심을 기울일 수 있다.
또한, Gaussian kernel에 대한 학습 가능한 스케일 파라미터 \(\sigma\)를 사용하여 prior-association이 다양한 시계열 패턴에 적응할 수 있도록 한다. ex) 다른 길이의 anomaly segments
series-association branch는 raw series로부터 연관성을 학습하는 것으로, 가장 효과적인 연관성을 적응적으로 찾을 수 있다.
이 두 branch는 각 시간 점의 시간적 종속성을 유지하며, 이는 point-wise 표현보다 정보가 더 많다.
또한, 두 branch는 각각 adjacent-concentration prior 및 학습된 실제 연관성을 반영하고, adjacent-concentration prior과 학습된 실제 연관성의 discrepancy는 정상-비정상을 구별할 수 있을 것이다.
\(l\)번째 레이어의 Anomaly-Attention는 다음과 같다.
\[\begin{equation} \begin{split} \text{Initialization: } & Q, K, V, \sigma = X^{l-1}W^l_Q, X^{l-1}W^l_K, X^{l-1}W^l_V, X^{l-1}W^l_\sigma \\ \text{Prior-Association: } & P^l = \text{Rescale}\Bigg(\left[\frac{1}{\sqrt{2\pi}\sigma_i} \exp\bigg(- \frac{|j - i|^2}{2\sigma_i^2} \bigg)\right]_{i, j \in {1, ..., N}}\Bigg) \\ \text{Series-Association: } & S^l = \text{Softmax}\left(\frac{QK^T}{\sqrt{d_\text{model}}}\right) \\ \text{Reconstruction: } & \hat{X}^l = S^lV \end{split} \label{eq:eq2} \end{equation}\]여기서 \(Q, K, V \in \mathbb{R}^{N×d_\text{model}} , \sigma ∈ \mathbb{R}^{N×1}\)는 각각 self-attention의 query, key, value 및 학습된 스케일을 나타낸다.
\(W^l_Q, W^l_K, W^l_V \in \mathbb{R}^{d_\text{model}×d_\text{model}}, W^l_\sigma \in \mathbb{R}^{d_\text{model}×1}\) 각각은 \(l\)번째 레이어에서 \(Q, K, V, \sigma\)에 대한 매개변수 행렬을 나타낸다.
Prior-association \(P^l \in \mathbb{R}^{N×N}\)은 학습된 스케일 \(\sigma \in \mathbb{R}^{N×1}\)에 기반하며, \(i\)번째 요소 \(\sigma_i\)는 \(i\)번째 시간 점에 해당한다.
구체적으로, \(i\)번째 시간 점에 대해 \(j\)번째 점의 association weight는 거리 \(|j − i|\)에 대해 Gaussian kernel \(G(|j − i|; σ_i) = \frac{1}{\sqrt{2\pi}\sigma_i} \exp(−\frac{|j−i|^2}{2σ^2_i})\)에 따라 계산된다.
더 나아가, \(\text{Rescale}(·)\)을 사용하여 행 합으로 나누어 association weight를 이산 분포 \(P^l\)로 변환한다.
\(S^l \in \mathbb{R}^{N×N}\)은 series-association을 나타낸다.
\(\text{Softmax}(·)\)은 마지막 차원을 따라 attention map을 정규화한다.
따라서, \(S^l\)의 각 행은 이산 분포를 형성한다.
\(\hat{Z}^l \in \mathbb{R}^{N×d_\text{model}}\) 은 \(l\)번째 레이어의 Anomaly-Attention 이후의 숨겨진 표현이다.
\(\text{Anomaly-Attention}(·)\)을 사용하여 \eqref{eq:eq2}를 요약된다.
여기서 사용되는 multi-head version에서 학습된 스케일은 \(h\) 헤드에 대해 \(\sigma \in \mathbb{R}^{N×h}\) 이다.
\(Q_m, K_m, V_m \in \mathbb{R}^{N×\frac{d_\text{model}}{h}}\)는 각각 \(m\)번째 헤드의 query, key 및 value이다.
블록은 여러 헤드의 출력 \(\{\hat{Z}^l_m \in \mathbb{R}^{N×\frac{d_\text{model}}{h}} \}_{1≤m≤h}\)를 연결하고 최종 결과 \(\hat{Z}^l \in \mathbb{R}^{N×d_\text{model}}\)를 얻는다.
Association Discrepancy
prior-association과 series-association 사이의 symmetrized KL divergence으로 information gain을 나타내는 Association Discrepancy을 형식화했다.
다중 레이어에서의 association discrepancy을 평균하여, 다중 레벨 특징에서의 association을 더 많은 정보를 담은 측정으로 결합했다:
여기서 \(\text{KL}(·\|·)\)는 \(P^l\)과 \(S^l\)의 각 행에 해당하는 두 이산 분포 사이의 KL 발산을 계산한다. \(\text{AssDis}(P, S; X ) \in \mathbb{R}^{N×1}\) 은 \(X\)의 prior-association \(P\) 및 series-association \(S\)에 대한 다중 레이어의 point-wise association discrepancy이다.
결과의 \(i\)번째 요소는 \(X\)의 \(i\)번째 시간 점에 해당된다.
이전 관측 결과, 이상점은 \(\text{AssDis}(P, S; X )\)가 정상 시간 점보다 작게 나타날 것이며, 이는 \(\text{AssDis}\) 본질적으로 구별 가능하게 만든다.
3.2 Minimax Association Learning
비지도 학습 과제로, 우리는 모델을 최적화하기 위해 reconstruction loss을 사용한다.
reconstruction loss은 series-association이 가장 정보를 제공하는 연관을 찾도록 안내한다.
정상 및 이상점 사이의 차이를 더 크게 만들기 위해, 우리는 association discrepancy을 확대하기 위해 추가 손실을 사용한다. prior-association의 unimodal 특성으로 인해, discrepancy loss은 series-association이 비인접 영역에 더 많은 관심을 기울이도록 안내한다. 이는 이상점의 reconstruction을 어렵게 만들고 이상점을 더 잘 식별할 수 있도록 한다. 입력 시리즈 \(X \in \mathbb{R}^{N×d}\)의 손실 함수는 다음과 같이 같다:
여기서 \(\hat{X} \in \mathbb{R}^{N×d}\)는 \(X\)의 reconstruction을 나타낸다.
\(\|·\|_F\), \(\|·\|_k\) 는 Frobenius 및 k-norm 나타낸다. \(\lambda\)는 손실 항목을 교환하는 역할을 한다. \(\lambda > 0\)일 때, 최적화는 association discrepancy을 확대하는 것이다.
association discrepancy을 더 구별 가능하게 만들기 위해 minimax 전략이 제안된다.
Minimax Strategy
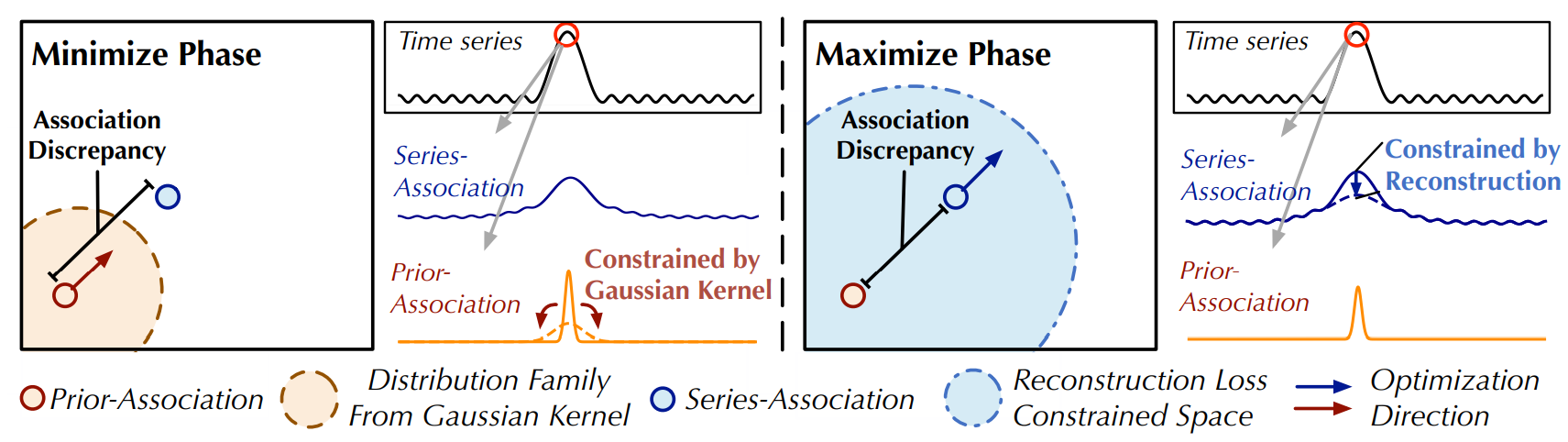직접적으로 association discrepancy을 최대화하는 것은 Gaussian kernel의 스케일 매개변수를 극도로 줄일 것이다, 이는 prior-association을 무의미하게 만든다.
association 학습을 더 잘 제어하기 위해 minimax 전략을 제안한다.
구체적으로, 최소화 단계에서는 우리가 prior-association \(P^l\)을 raw series에서 학습된 series-association \(S^l\)에 근사하도록 이끈다.
이 과정은 prior-association이 다양한 시간적 패턴에 적응하도록 만든다.
최대화 단계에서는 series-association을 최적화하여 association discrepancy을 확대한다.
이 과정은 series-association이 비인접 지점에 더 많은 관심을 기울이도록 만든다.
따라서, reconstruction loss을 통합하여, 두 단계의 손실 함수는 다음과 같다:
여기서 \(\lambda > 0\) 이고 \(∗_{\text{detach}}\) 는 association의 gradient backpropagation를 중지하는 것을 의미한다.
최소화 단계에서 \(P\)가 \(S_{\text{detach}}\)를 근사하면, 최대화 단계에서는 series-association에 더 강한 제약을 가해 시간 점들이 비인접 영역에 더 많은 관심을 기울이도록 한다.
reconstruction loss 하에서, 이는 이상점이 정상 시간 점보다 훨씬 어려운 것이며, 이로써 association discrepancy의 정상-이상 구별 가능성을 증폭시킨다.
Association-based Anomaly Criterion
reconstruction 기준에 정규화된 association discrepancy을 통합했다. 이건 시간적 표현과 구별 가능한 association discrepancy의 이점을 모두 취할 것이다.
\(X \in \mathbb{R}^{N×d}\)의 최종 이상 점수는 다음과 같이 나타난다:
여기서 \(\odot\)는 element-wise multiplication이다.
\(\text{AnomalyScore} (X ) \in \mathbb{R}^{N×1}\) 은 \(X\)의 점 단위 이상 기준을 나타낸다.
더 나은 재구성을 위해, 이상점은 보통 association discrepancy을 감소시키는데, 이는 여전히 더 높은 이상 점수를 유도한다.
따라서, 이 설계는 reconstruction error와 association discrepancy이 협력하여 탐지 성능을 개선할 수 있도록 한다.
4 Experiments
Datasets
데이터셋은 인터넷 기업, NASA, eBay, 그리고 핵심 인프라 시스템과 같은 다양한 소스에서 비롯되었으며, NeurIPS-TS는 분류된 이상 케이스를 제공한다.
Implementation details
- 모든 데이터셋에 대해 크기 100의 중첩되지 않는 슬라이딩 윈도우 접근법 사용
- 점수가 임계값 \(\delta\)를 초과하면 이상으로 표시되며, 이 임계값은 검증 데이터셋의 일정 비율을 이상으로 표시하기 위해 설정
- SWaT의 경우 0.1%, SMD의 경우 0.5%, 다른 데이터셋의 경우 1%
- 시간 내에서 이상점이 발견되면 해당 이상적인 세그먼트 전체를 감지된 것으로 표시하는 널리 사용되는 조정 전략 적용
- Anomaly Transformer는 3개의 레이어로 구성되며, \(d_{\text{model}}\)은 512로 설정되고 \(h\)는 8로 설정됨
- 모든 데이터셋에 대해 하이퍼파라미터 \(\lambda\)가 3으로 설정됨
- 초기 학습률이 \(10^{-4}\)인 ADAM 옵티마이저를 사용하여 학습하며, 배치 크기는 32로 설정되고 10 epochs 이내 조기 중단
- 단일 NVIDIA TITAN RTX 24GB GPU에서 PyTorch로 구현.
Baselines
- 다양한 접근 방식에서 18개의 기준선과의 철저한 비교 실시:
- Reconstruction-based 모델: InterFusion, BeatGAN, OmniAnomaly, LSTM-VAE
- Density-estimation 모델: DAGMM, MPPCACD, LOF
- 클러스터링 기반 방법: ITAD, THOC, Deep-SVDD
- Autoregression-based 모델: CL-MPPCA, LSTM, VAR
- 클래식 방법: OC-SVM, IsolationForest
- 추가적인 세 개의 기준선은 변화점 탐지 및 시계열 분할에서 고려
- InterFusion과 THOC가 baseline 중 SOTA
4.1 Main Results
Real-world datasets
10 개의 baseline을 사용하여 다섯 개의 실제 데이터셋에서 우리의 모델을 철저히 평가했다.
비정상 탐지를 위한 시간 모델링과 연관 학습의 효과를 입증하여, Anomaly Transformer가 모든 벤치마크에서 일관된 SOTA을 달성했다.
ROC 곡선은 다양한 임계값에 대한 Anomaly Transformer의 뛰어난 성능을 확인하여 실제 응용 가능성을 강조하고 있다.
NeurIPS-TS benchmark
이 벤치마크는 모든 이상점 유형을 포괄하며, 지점 및 패턴에 따른 이상점을 모두 포함한다.
그럼에도 불구하고, Anomaly Transformer는 여전히 SOTA을 달성할 수 있다.
이는 다양한 이상점 유형에 대한 Anomaly Transformer의 효과를 입증했다고 할 수 있다.
Ablation study
table 2에서 모델의 각 부분의 영향을 분석했다.
association-based criterion은 일관되게 널리 사용되는 reconstruction 기준보다 우수한 성능을 보이며, 높은 18.76%의 절대 F1-score 향상을 이끌었다.
association discrepancy를 기준으로 사용하는 것만으로도 우수한 성능을 보이며, 이전 SOTA 모델을 뛰어넘는다.
학습 가능한 prior-association과 minimax 전략을 도입하여 Anomaly Transformer 모델을 더욱 향상시켰다. 마지막으로, Anomaly Transformer는 순수한 Transformer보다 18.34%의 절대적인 개선을 달성했다.
4.2 Model Analysis
Anomaly criterion visualization
Figure 5에서는 다양한 이상점 유형에 대한 association-based 기준의 성능을 시각화한 것을 제공한다.
reconstruction 기준과 비교하여 우리 방법은 일관되게 정상 데이터에 대해 더 작은 값이 생성되며 이상점을 효과적으로 강조하고, 이 정밀성은 거짓 양성을 줄여 전체 감지 정확도를 향상시킨다.
Prior-association visualization
minimax 최적화 과정에서 학습된 prior-association은 series-association에 가까워지도록 하여, 학습된 매개변수 \(\sigma\)는 시계열 내 인접한 점의 집중도를 반영할 수 있다.
그림 6에서 볼 수 있듯이, \(\sigma\)는 다양한 데이터 패턴에 적응하여 변화한다.
특히, 이상점의 prior-association은 일반적으로 정상 시간점보다 작은 \(\sigma\)를 갖는 경향이 있다.
이는 이상점이 더 높은 인접 집중도를 보일 것으로 예상되는 것과 일치한다.
Optimization strategy analysis
reconstruction loss만 사용할 경우, 이상 및 정상 시간점은 이웃 시간점에 대해 유사한 association 가중치를 보여 대조 값이 1에 가깝다(Table 3).
association discrepancy를 최대화하면 시계열 연관은 이웃이 아닌 영역에 주의를 기울이도록 한다.
그러나 더 나은 reconstruction을 위해, 이상점은 정상 시간점보다 훨씬 큰 이웃 연관 가중치를 유지해야 한다.
이는 더 큰 대조 값을 가져온다.
직접 최대화는 정상과 이상 시간점 간의 차이를 효과적으로 증폭시키기 어렵다.
minimax 전략은 prior-association을 최적화하여 시계열 연관에 더 강력한 제약을 제공하므로, 더 구별 가능한 대조 값을 얻어 성능이 향상된다.
5 Conclusion and Future Work
이 논문은 비지도 시계열 이상 감지를 위해 Anomaly Transformer를 소개했다.
Transformer를 활용하여 정보를 풍부하게 포착하기 위해 time-point association을 학습했다.
Anomaly-Attention과 minimax 전략을 통합하여 이상 감지를 향상시켰다.
이 방법은 실험적 연구에서 SOTA를 달성하며, 미래에는 이상 감지기를 autoregression 및 state space model 분석과 관련하여 이론적으로 탐구될 예정이다.
Next: Anomaly Transformer(2)