Anomaly Transformer(2)

논문: Anomaly Transformer: Time Series Anomaly Detection with Association Discrepancy

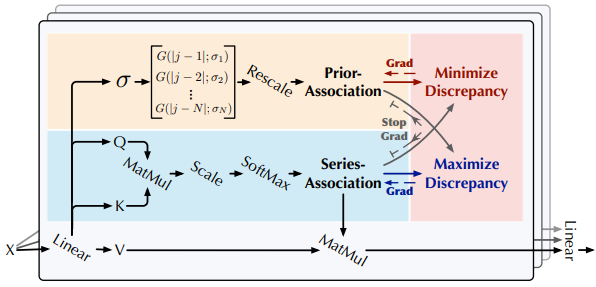
Anomaly Transformer: 트랜스포머를 활용하는 비지도 시계열 이상 감지 모델

• Association Discrepancy를 도입하여 정상과 비정상 점 구별
• Anomaly-Attention 메커니즘을 통해 Association Discrepancy 계산
• Minimax 전략으로 모델의 이상 감지 능력 향상

사전 지식

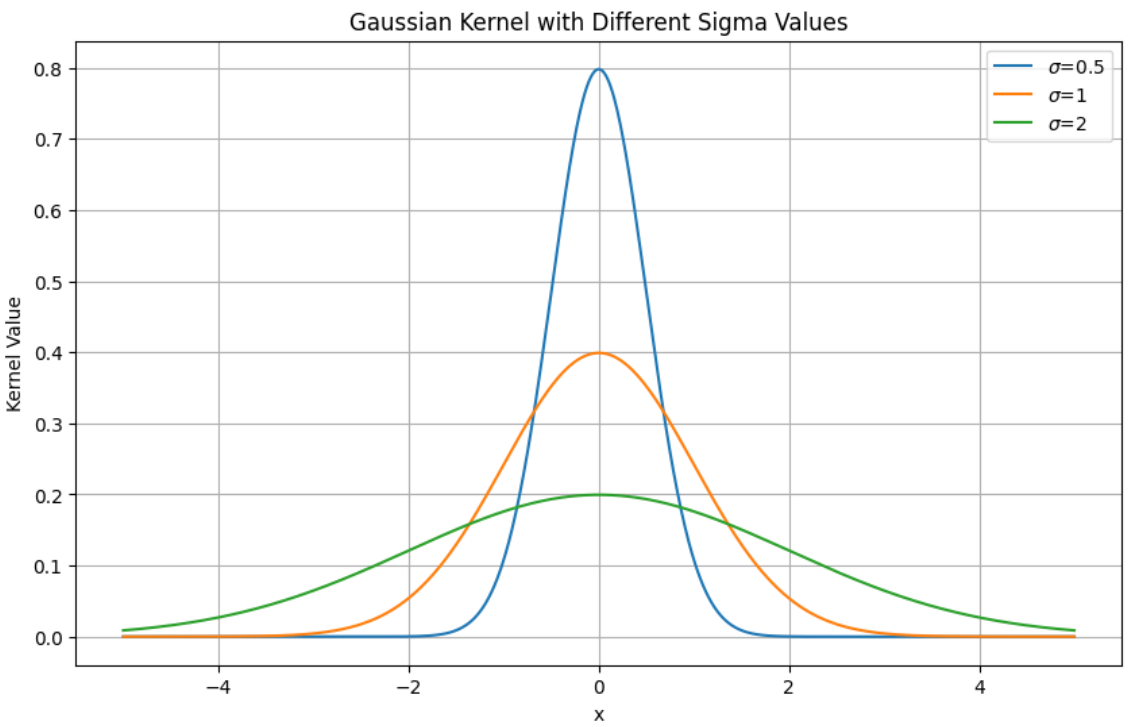
Gaussian kernel

연속 데이터의 평활화, 필터링 및 모델링에 사용

\[K(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{x^2}{2\sigma^2}}\]

• \(x\) 는 중심으로부터의 거리
• \(\sigma\) 는 표준 편차로, 커널의 폭이나 너비를 결정

Gaussian kernel은 이웃한 점에 가중치를 할당하며, 가까운 점은 높은 가중치를 받고 먼 점은 낮은 가중치를 받는다.
Anomaly Transformer은 연속성으로 인해 이상점이 인근 시간점에서 더 자주 발생할 가능성이 높은 adjacent-concentration inductive bias을 포착할 수 있다.

adjacent-concentration inductive bias: 시계열 데이터셋 내에서 이상점이 이웃하거나 인접한 시간 지점에 군집하는 경향

Unimodal(단봉성): 분포, 함수 또는 데이터 집합이 하나의 봉우리 또는 모드를 가지고 있는 것

Symmetrized KL Divergence

Kullback-Leibler(KL) divergence(이하 KL 발산)은 두 확률 분포 간의 차이를 측정하는 방법이다.

\[D_{KL}(P \| Q) = \sum_{i} P(i) \log \frac{P(i)}{Q(i)}\]

두 분포 \(P\) 와 \(Q\) 사이의 KL 발산은 한 분포가 다른 분포로부터 얼마나 멀어지는지를 측정한다.
그러나 이는 비대칭적이며, 즉 \(KL(P \| Q)\) 가 반드시 \(KL(Q \| P)\) 와 같지 않다.

대칭 KL 발산은 이러한 비대칭성을 극복하기 위해 두 방향으로 계산된 KL 발산의 평균을 취한다:

\[KL(P, Q) = \frac{1}{2} \bigg( KL(P \| Q) + KL(Q \| P) \bigg)\]

Anomaly Transformer에서 대칭 KL 발산은 prior-association과 series-association 분포 사이의 불일치를 나타내는 Association Discrepancy의 측정에 활용된다.
이 불일치는 시계열 데이터에서 정상과 비정상 점을 구별하는 데 도움된다.

Example

Sample Data

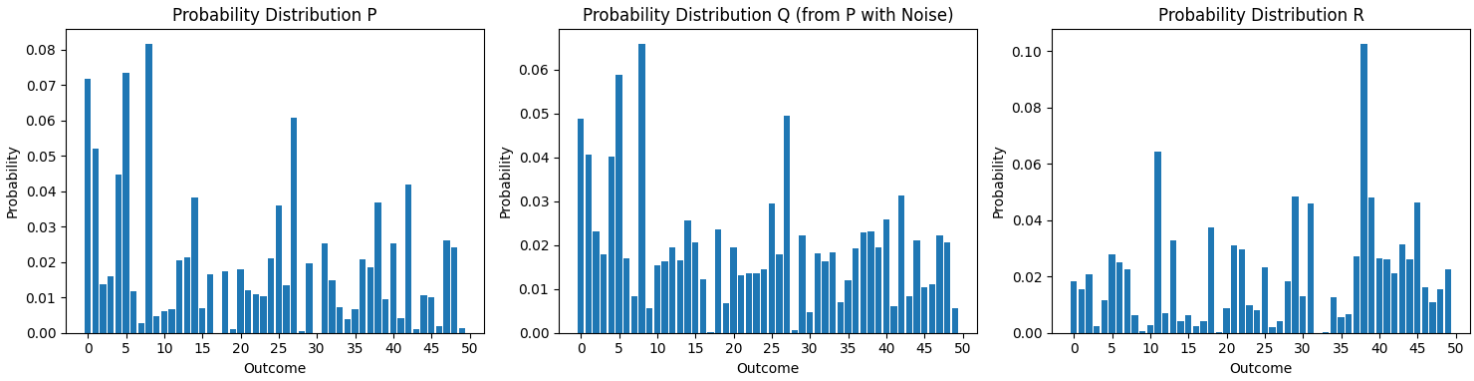
\(P\): 랜덤 확률 분포
\(Q\): \(P\) 에 노이즈 추가
\(R\): 랜덤 확률 분포

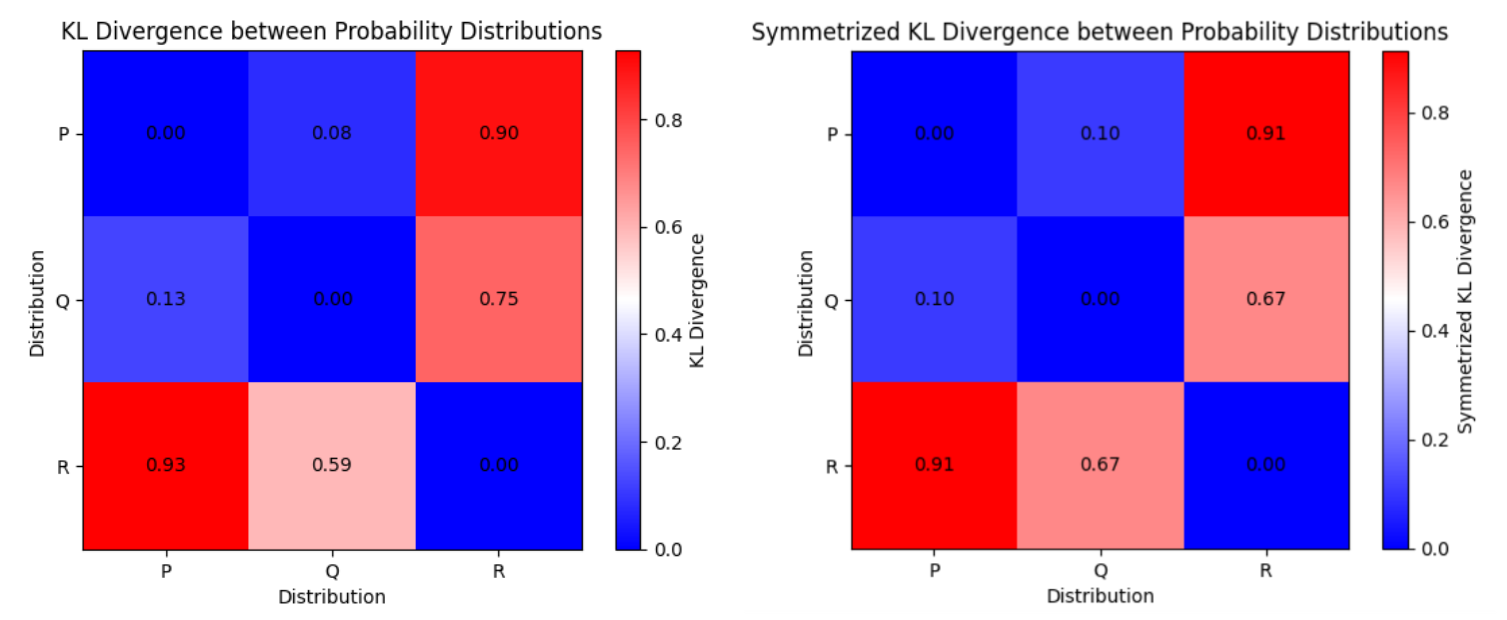
KL 분산 및 대칭 KL 분산

def kl_divergence(p, q):
    kl_div = np.sum(np.where(p != 0, p * np.log(p / q), 0))
    return kl_div

def symmetrized_kl_divergence(p, q):
    sym_kl_div = 0.5 * (kl_divergence(p, q) + kl_divergence(q, p))
    return sym_kl_div

Norm

Frobenius Norm

뉴클리드 Norm

\[\| A \|_F = \sqrt{\sum_{i,j} |a_{ij}|^2}\]

k-Norm

Frobenius norm의 일반화

\[\| A \|_k = \left( \sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^k \right)^{\frac{1}{k}}\]

\(k = 2\): Frobenius norm
\(k = 1\): \(L_1\) norm 또는 Manhattan norm
\(k = \infty\): \(L_{\infty}\) norm 또는 최대 norm

---

Next: Anomaly Transformer(3)