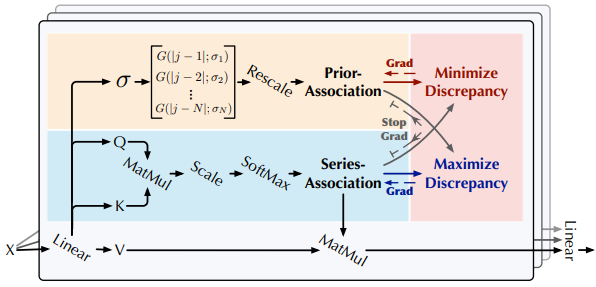
Anomaly Transformer(3)
논문: Anomaly Transformer: Time Series Anomaly Detection with Association Discrepancy
코드:https://github.com/thuml/Anomaly-Transformer
Anomaly Transformer의 공식 코드를 확인해봤다.
구성
main.py: config 값을 받고, Solver의 train 또는 test 실행
solver.py: 데이터 로드, 모델 빌드 및 train, valid 또는 test 수행
data_factory/data_loader.py: 각 데이터셋에 대한 전처리(scaler 적용, __getitem__ 정의) 및 DataLoader 구축
model/AnomalyTransformer.py: EncoderLayer, Encoder, AnomalyTransformer 아키텍쳐 정의
model/attn.py: AnomalyAttention, AttentionLayer 아키텍쳐 정의
model/embed.py: PositionalEmbedding, TokenEmbedding, DataEmbedding 아키텍쳐 정의
utils/logger.py: 로깅 기능 구현
utils/utils.py: 기타 편의 기능 구현
아키텍쳐
배치 크기가 \(B\), 길이가 \(L\)이고 \(c_{\text{in}}\)개의 측정값으로 이루어진 시계열 \(X \in \mathbb{R}^{B×L×c_{\text{in}}}\)를 입력
embed.py
PositionalEmbedding
시퀀스의 토큰에 대한 위치 임베딩을 계산
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class PositionalEmbedding(nn.Module):
def __init__(self, d_model, max_len=5000):
super(PositionalEmbedding, self).__init__()
# Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model).float()
# 역전파 중에 이 텐서에 대한 그라디언트가 계산되지 않음
pe.require_grad = False
position = (
torch.arange(0, max_len).float()
.unsqueeze(1) # (max_len) -> (max_len, 1)
)
div_term = (torch.arange(0, d_model, 2).float() *
-(math.log(10000.0) / d_model)).exp()
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0) # (max_len, d_model) -> (1, max_len, d_model)
# pe를 Module의 buffer로 등록
# buffer는 그라디언트를 계산할 때 고려되지 않지만
# 모델의 상태의 일부로 유지되는 매개변수
self.register_buffer('pe', pe)
def forward(self, x):
return self.pe[:, :x.size(1)] # (1, max_len, d_model) -> (1, L, d_model)
Input: \(X \in \mathbb{R}^{B×L×c_{\text{in}}}\)
Output: \(\text{PE}(X) \in \mathbb{R}^{1×L×d_{\text{model}}}\)
Buffer
- 특징
- 훈련 가능한 매개변수로 간주되지 않음
- 계산에 필요한 상수 또는 사전에 계산된 값과 같은 중요한 정보를 저장
- 모듈의 상태의 일부이며 모델의 매개변수와 함께 저장되고 복원
- Buffer 액세스
- 지정된 이름을 사용하여 모듈의 속성으로 버퍼에 액세스 가능
- 훈련 및 추론 중에 액세스 가능
- 저장 및 로드
- 모델을 저장하거나 로드할 때 state dictionary에 버퍼가 포함되어 모델 체크포인트 간에 보존
TokenEmbedding
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class TokenEmbedding(nn.Module):
def __init__(self, c_in, d_model):
super(TokenEmbedding, self).__init__()
# PyTorch 1.5.0 버전 이후에 circular padding의 작동 방식이 변함
padding = 1 if torch.__version__ >= '1.5.0' else 2
self.tokenConv = nn.Conv1d(
in_channels=c_in, out_channels=d_model,
kernel_size=3, padding=padding,
padding_mode='circular', bias=False
) # tokenConv weight size: (d_model, c_in, kernel)
for m in self.modules():
if isinstance(m, nn.Conv1d):
nn.init.kaiming_normal_(m.weight, mode='fan_in',
nonlinearity='leaky_relu')
def forward(self, x):
x = self.tokenConv(
x.permute(0, 2, 1) # (B, L, c_in) -> (B, c_in, L)
) # (B, c_in, L) -> (B, d_model, L)
x = x.transpose(1, 2) # (B, d_model, L) -> (B, L, d_model)
return x
Input: \(X \in \mathbb{R}^{B×L×c_{\text{in}}}\)
Output: \(\text{Token-Embedding}(X) \in \mathbb{R}^{B×L×d_{\text{model}}}\)
DataEmbedding
1
2
3
4
5
6
7
8
9
10
11
12
class DataEmbedding(nn.Module):
def __init__(self, c_in, d_model, dropout=0.0):
super(DataEmbedding, self).__init__()
self.value_embedding = TokenEmbedding(c_in=c_in, d_model=d_model)
self.position_embedding = PositionalEmbedding(d_model=d_model)
self.dropout = nn.Dropout(p=dropout)
def forward(self, x):
x = self.value_embedding(x) + self.position_embedding(x)
return self.dropout(x)
Input: \(X \in \mathbb{R}^{B×L×c_{\text{in}}}\)
Output: \(X^0 = \text{Dropout} \big(\text{Token-Embedding}(X) \oplus \text{PE}(X)\big) \in \mathbb{R}^{B×L×d_{\text{model}}}\)
attn.py
AttentionLayer
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class AttentionLayer(nn.Module):
def __init__(self, attention, d_model, n_heads, d_keys=None,
d_values=None):
super(AttentionLayer, self).__init__()
d_keys = d_keys or (d_model // n_heads)
d_values = d_values or (d_model // n_heads)
self.norm = nn.LayerNorm(d_model)
self.inner_attention = attention
self.query_projection = nn.Linear(d_model,
d_keys * n_heads)
self.key_projection = nn.Linear(d_model,
d_keys * n_heads)
self.value_projection = nn.Linear(d_model,
d_values * n_heads)
self.sigma_projection = nn.Linear(d_model,
n_heads)
self.out_projection = nn.Linear(d_values * n_heads, d_model)
self.n_heads = n_heads
def forward(self, queries, keys, values, attn_mask):
B, L, _ = queries.shape
_, S, _ = keys.shape
H = self.n_heads
x = queries
# d_model = d_keys*H
queries = (
self.query_projection(queries) # (B, L, d_model), (d_keys*H, d_model) -> (B, L, d_keys*H)
.view(B, L, H, -1) # (B, L, d_keys*H) -> (B, L, H, d_keys)
)
keys = (
self.key_projection(keys) # (B, L, d_model), (d_keys*H, d_model) -> (B, L, d_keys*H)
.view(B, S, H, -1) # (B, L, d_keys*H) -> (B, L, H, d_keys)
)
# d_model = d_values*H
values = (
self.value_projection(values) # (B, L, d_model), (d_values*H, d_model) -> (B, L, d_values*H)
.view(B, S, H, -1) # (B, L, d_values*H) -> (B, L, H, d_values)
)
sigma = (
self.sigma_projection(x) # (B, L, d_model), (H, d_model) -> (B, L, H)
.view(B, L, H)
)
out, series, prior, sigma = self.inner_attention(
queries,
keys,
values,
sigma,
attn_mask
)
out = out.view(B, L, -1) # B L H D -> B L H*D i.e. (B, L, H, d_values) -> (B, L, d_values*H)
return self.out_projection(out), series, prior, sigma
# y: (B, L, d_values*H), (d_model, d_values*H) -> (B, L, d_model)
Input:
queries: \(X^{l-1} \in \mathbb{R}^{B×L×d_{\text{model}}}\)keys: \(X^{l-1} \in \mathbb{R}^{B×L×d_{\text{model}}}\)values: \(X^{l-1} \in \mathbb{R}^{B×L×d_{\text{model}}}\)
AnomalyAttention 먼저 확인
Output:
y: \(\hat{X}^l W^l_{\text{out projection}} \in \mathbb{R}^{B×L×d_{\text{model}}}\)series: \(S^l = \text{Softmax}\left(\frac{QK^T}{\sqrt{d_\text{model}}}\right) \in \mathbb{R}^{B×H×L×L}\)prior: \(P^l = \left[ \frac{1}{\sqrt{2\pi}\sigma_i} \exp\big( -\frac{\vert j - i\vert ^2}{2\sigma_i^2} \big)\right]_{i, j \in {1, ..., N}} \in \mathbb{R}^{B×H×L×L}\)sigma: \(\sigma^{(L)} \in \mathbb{R}^{B×H×L×L}\)
AnomalyAttention
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class AnomalyAttention(nn.Module):
def __init__(self, win_size, mask_flag=True, scale=None,
attention_dropout=0.0, output_attention=False):
super(AnomalyAttention, self).__init__()
self.scale = scale
self.mask_flag = mask_flag
self.output_attention = output_attention
self.dropout = nn.Dropout(attention_dropout)
window_size = win_size
self.distances = torch.zeros((window_size, window_size)).cuda()
for i in range(window_size):
for j in range(window_size):
self.distances[i][j] = abs(i - j)
def forward(self, queries, keys, values, sigma, attn_mask):
B, L, H, E = queries.shape
_, S, _, D = values.shape
# scale = self.scale if self.scale else 1. / sqrt(E)
scale = self.scale or 1. / sqrt(E)
scores = torch.einsum("blhe,bshe->bhls", queries, keys)
if self.mask_flag:
if attn_mask is None:
attn_mask = TriangularCausalMask(B, L, device=queries.device)
scores.masked_fill_(attn_mask.mask, -np.inf)
attn = scale * scores
sigma = sigma.transpose(1, 2) # B L H -> B H L
window_size = attn.shape[-1]
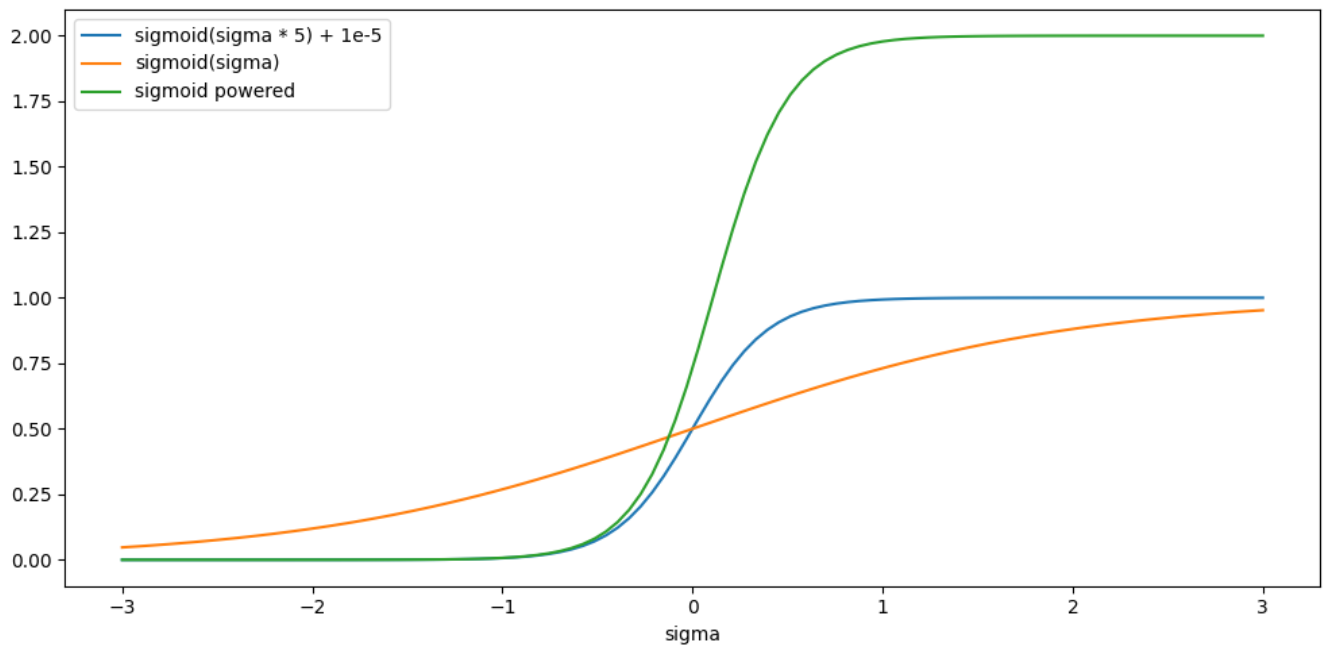
sigma = torch.sigmoid(sigma * 5) + 1e-5 # avoid potential division by zero
sigma = torch.pow(3, sigma) - 1
sigma = (
sigma.unsqueeze(-1) # B H L -> B H L 1
.repeat(1, 1, 1, window_size)
) # B H L L
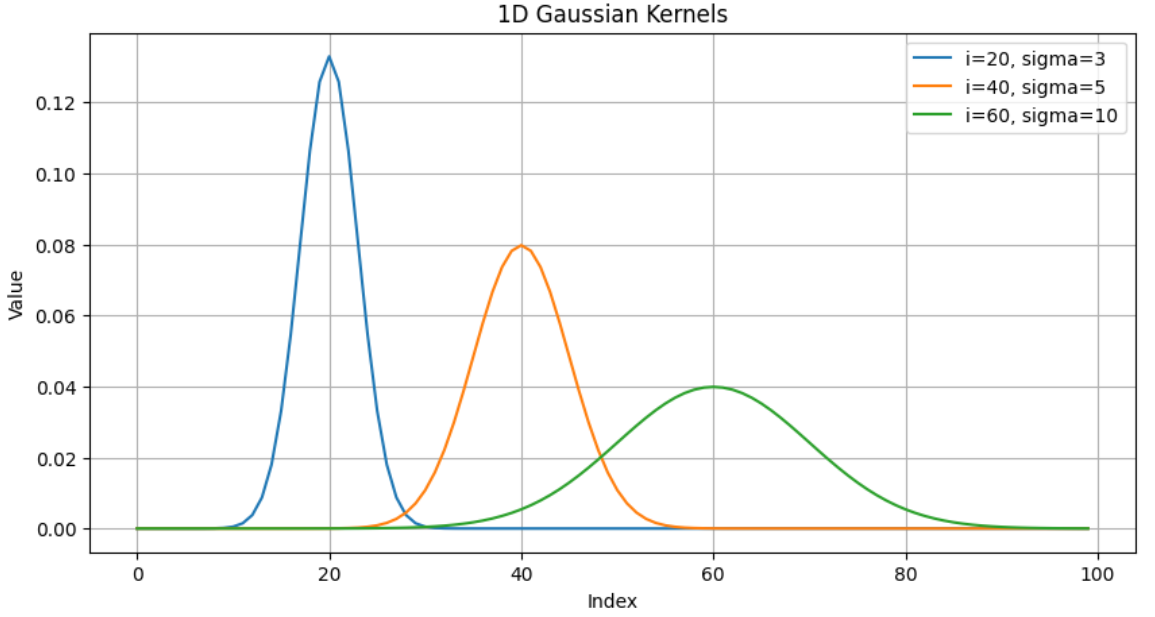
prior = (
self.distances # L L
.unsqueeze(0).unsqueeze(0) # 1 1 L L
.repeat(sigma.shape[0], sigma.shape[1], 1, 1) # B H L L
.cuda()
)
prior = 1.0 / (math.sqrt(2 * math.pi) * sigma) * \
torch.exp(-prior ** 2 / 2 / (sigma ** 2))
series = self.dropout(torch.softmax(attn, dim=-1))
V = torch.einsum("bhls,bshd->blhd", series, values)
if self.output_attention:
return (V.contiguous(), series, prior, sigma)
else:
return (V.contiguous(), None)
Input:
queries: \(Q = X^{l-1}W^l_Q \in \mathbb{R}^{B×L×H×d_{\text{keys}}}\)keys: \(K = X^{l-1}W^l_K \in \mathbb{R}^{B×L×H×d_{\text{keys}}}\)values: \(V = X^{l-1}W^l_V \in \mathbb{R}^{B×L×H×d_{\text{values}}}\)sigma: \(\sigma = X^{l-1}W^l_\sigma \in \mathbb{R}^{B×L×H}\)
Output:
V: \(\hat{X}^l = S^lV \in \mathbb{R}^{B×L×H×d_{\text{values}}}\)series: \(S^l = \text{Softmax}\left(\frac{QK^T}{\sqrt{d_\text{model}}}\right) \in \mathbb{R}^{B×H×L×L}\)prior: \(P^l = \left[ \frac{1}{\sqrt{2\pi}\sigma_i} \exp\big( -\frac{\vert j - i\vert ^2}{2\sigma_i^2} \big)\right]_{i, j \in {1, ..., N}} \in \mathbb{R}^{B×H×L×L}\)sigma: \(\sigma^{(L)} \in \mathbb{R}^{B×H×L×L}\)
sigma
prior
AnomalyTransformer.py
EncoderLayer
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class EncoderLayer(nn.Module):
def __init__(self, attention, d_model, d_ff=None, dropout=0.1, activation="relu"):
super(EncoderLayer, self).__init__()
d_ff = d_ff or 4 * d_model
self.attention = attention
self.conv1 = nn.Conv1d(in_channels=d_model, out_channels=d_ff, kernel_size=1)
self.conv2 = nn.Conv1d(in_channels=d_ff, out_channels=d_model, kernel_size=1)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.dropout = nn.Dropout(dropout)
self.activation = F.relu if activation == "relu" else F.gelu
def forward(self, x, attn_mask=None):
new_x, attn, mask, sigma = self.attention(
x, x, x,
attn_mask=attn_mask
)
x = x + self.dropout(new_x)
y = x = self.norm1(x)
y = self.dropout(self.activation(self.conv1(y.transpose(-1, 1))))
y = self.dropout(self.conv2(y).transpose(-1, 1))
return self.norm2(x + y), attn, mask, sigma
Input: \(X^{l-1} \in \mathbb{R}^{B×L×d_{\text{model}}}\)
y: \(Z^l = \text{Layer-Norm}(\text{Anomaly-Attention}(X^{l-1}) + X^{l-1})\)
Output: \(X^l = \text{Layer-Norm}(\text{Feed-Forward}(Z^{l}) + Z^{l}) \in \mathbb{R}^{B×L×d_{\text{model}}}\)
Encoder
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Encoder(nn.Module):
def __init__(self, attn_layers, norm_layer=None):
super(Encoder, self).__init__()
self.attn_layers = nn.ModuleList(attn_layers)
self.norm = norm_layer
def forward(self, x, attn_mask=None):
# x [B, L, D]
series_list = []
prior_list = []
sigma_list = []
for attn_layer in self.attn_layers:
x, series, prior, sigma = attn_layer(x, attn_mask=attn_mask)
series_list.append(series)
prior_list.append(prior)
sigma_list.append(sigma)
if self.norm is not None:
x = self.norm(x)
return x, series_list, prior_list, sigma_list
AnomalyTransformer
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class AnomalyTransformer(nn.Module):
def __init__(self, win_size, enc_in, c_out,
d_model=512, n_heads=8, e_layers=3, d_ff=512,
dropout=0.0, activation='gelu', output_attention=True):
super(AnomalyTransformer, self).__init__()
self.output_attention = output_attention
# Encoding
self.embedding = DataEmbedding(enc_in, d_model, dropout)
# Encoder
self.encoder = Encoder(
[
EncoderLayer(
AttentionLayer(
AnomalyAttention(win_size, False, attention_dropout=dropout, output_attention=output_attention),
d_model, n_heads),
d_model,
d_ff,
dropout=dropout,
activation=activation
) for l in range(e_layers)
],
norm_layer=torch.nn.LayerNorm(d_model)
)
self.projection = nn.Linear(d_model, c_out, bias=True)
def forward(self, x):
enc_out = self.embedding(x)
enc_out, series, prior, sigmas = self.encoder(enc_out)
enc_out = self.projection(enc_out)
if self.output_attention:
return enc_out, series, prior, sigmas
else:
return enc_out # [B, L, D]
훈련
sovler.py
Solver.train()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
def train(self):
path = self.model_save_path
if not os.path.exists(path):
os.makedirs(path)
early_stopping = EarlyStopping(patience=3, verbose=True, dataset_name=self.dataset)
train_steps = len(self.train_loader)
for epoch in range(self.num_epochs):
iter_count = 0
loss1_list = []
epoch_time = time.time()
self.model.train()
for i, (input_data, labels) in enumerate(self.train_loader):
self.optimizer.zero_grad()
iter_count += 1
input = input_data.float().to(self.device)
output, series, prior, _ = self.model(input)
# calculate Association discrepancy
series_loss = 0.0
prior_loss = 0.0
for u in range(len(prior)):
series_loss += (
torch.mean(
my_kl_loss(
series[u],
(
prior[u] /
torch.unsqueeze(
torch.sum(prior[u], dim=-1),
dim=-1
).repeat(1, 1, 1, self.win_size)
).detach()
)
) + torch.mean(
my_kl_loss(
(
prior[u] /
torch.unsqueeze(
torch.sum(prior[u], dim=-1),
dim=-1
).repeat(1, 1, 1, self.win_size)
).detach(),
series[u]
)
)
)
prior_loss += (
torch.mean(
my_kl_loss(
(
prior[u] /
torch.unsqueeze(
torch.sum(prior[u], dim=-1),
dim=-1
).repeat(1, 1, 1, self.win_size)
),
series[u].detach()
)
) + torch.mean(
my_kl_loss(
series[u].detach(),
(
prior[u] /
torch.unsqueeze(
torch.sum(prior[u], dim=-1),
dim=-1
).repeat(1, 1, 1, self.win_size)
)
)
)
)
series_loss = series_loss / len(prior)
prior_loss = prior_loss / len(prior)
rec_loss = self.criterion(output, input)
loss1_list.append((rec_loss - self.k * series_loss).item())
loss1 = rec_loss - self.k * series_loss
loss2 = rec_loss + self.k * prior_loss
# Minimax strategy
loss1.backward(retain_graph=True)
loss2.backward()
self.optimizer.step()
print("Epoch: {} cost time: {}".format(epoch + 1, time.time() - epoch_time))
train_loss = np.average(loss1_list)
vali_loss1, vali_loss2 = self.vali(self.test_loader)
print(
"Epoch: {0}, Steps: {1} | Train Loss: {2:.7f} Vali Loss: {3:.7f} ".format(
epoch + 1, train_steps, train_loss, vali_loss1))
early_stopping(vali_loss1, vali_loss2, self.model, path)
if early_stopping.early_stop:
print("Early stopping")
break
adjust_learning_rate(self.optimizer, epoch + 1, self.lr)
Next: Anomaly Transformer(4)